まとめ:二等辺三角形の底辺は二等分線からはじまる。 二等辺三角形の底辺の計算は簡単。 頂角の二等分線を底辺にひく 底辺の半分の長さを求める そいつを2倍する っていう3ステップでいいんだ。 どんどん問題をといてみよう! そんじゃねー Ken 学校の先生に信じられないこと言われた底辺×高さ÷2 友だちの少ない長女は、休み時間よく先生と過ごしているようです。 ある日の先生と長女の会話。 ちなみに、先生は長女が先取りしていることを知っています。 先生「三角形の面積の出し方知っ 角柱の体積は、底面積×高さ で求められるかどうかは、まだわからない 縦×横×高さ÷2を、縦×横÷2×高さと 変形し、 長方形とは何かを学ぶ小学校2年生から、組み合わせの学習(コンビネーション)をする高校生まで授業で扱うことができます。 問題

台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
底辺×高さ÷2 何年生
底辺×高さ÷2 何年生- 直方体や立方体の公式の「たて×横×高さ」という公式は、一辺が\(1cm\)の立方体の数の数え方とみることができます。 ・小学5年生で習う体積の意味は?かさと何が違うの? 三角形の面積はなぜ底辺×高さ÷2なの?小5の学習ポイント4 辺の比と面積比 題材にして見ていきます。 今回も前回同様、内容が盛り沢山になっています。 それぞれの学習内容は非常に濃いものです。 半年以上も前のことなので忘れてしまっているケースもあるでしょう。 理解しやすいかも




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
先生「四角形は三角形2つなので四角形の面積を求めて2で割ればいいから、底辺×高さ÷2で導けます」 人間達「はーい! 」 イッチ「なんでや」 先生「では次の問題へ進みます」 人間達 底辺が6cm、高さが4cmの三角形は6×4÷2=12cm²になりますが、どうして三角形の面積は底辺×高さ÷2で求められるのでしょうか? かけ算の九九(三の段)|小学2年生・算数 立方体の表面積を求める計算と公式(辺と表面積の対応表つき)小学1年生から中学3年生までの教科書を物置から出して、取り憑かれたかのように読み漁りました。 底辺×高さ÷2を丸暗記してた当時の僕はその意味を知ることですべてが変わりました。 何が起こったのか? もう、それは書ききれないほどあります。
平行四辺形の面積=底辺×高さ 平行四辺形の周りの長さ=(縦+横)×2 ひし形の面積=対角線×もう一方の対角線÷2 ひし形の周りの長さ=一辺×4 バドミントン部1年生必見! なぜ、どんな形をした三角形でも、その面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求まるのでしょうか。 形がちがう2種類の「底辺 5 c m 高さ 2 c m の三角形」を通じてみていきましょう。 ※1マス 1 c m 初めに、同じ形直角三角形の底辺と斜辺から傾斜角と高さ 釣りをしていて、aを水深、cを出て行ったラインのm数として、仕掛けが船から何m離れたところにあるのかを知りたくて探していました。 三角形の3辺か
任意の辺を底辺とすることができる。底辺とそれに対する頂点との距離が高さで、「底辺(の長さ)×高さ÷2」で面積が求まる。 二等辺三角形 任意の辺を底辺とすることができるが、特に断らなければ、等しい2辺以外の3本目の辺を底辺とする。 直角三角形四角柱 ⇒ (上底下底)÷2×高さ×四角柱の高さ 四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 体積の求め方、覚え方 前述した体積の公式を使って、具体的に各図形の体積を計算します。 立方体の体積 下図が立方体です。立方体は全ての辺が同じ長さなの 受験問題集の〔斜辺×斜辺÷4〕って何? 30度の角度を持つ二等辺三角形の面積計算です。 スタンダードな解き方のほか、進学塾や高難度の受験問題集で用いられる「斜辺×斜辺÷4」の意味を解説しています。 お子様の中学受験を検討している保護者の方が



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



5年生算数 面積 黒板log
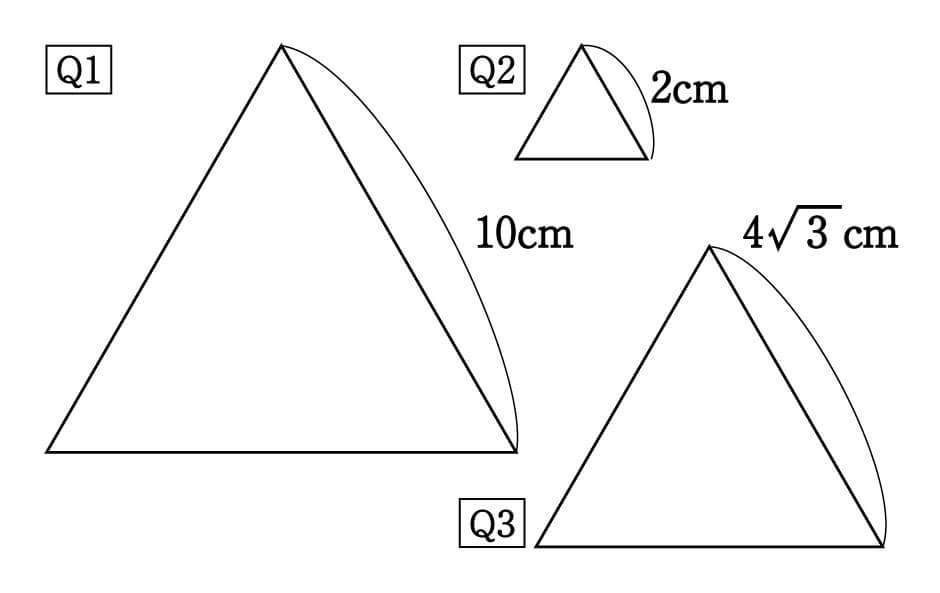
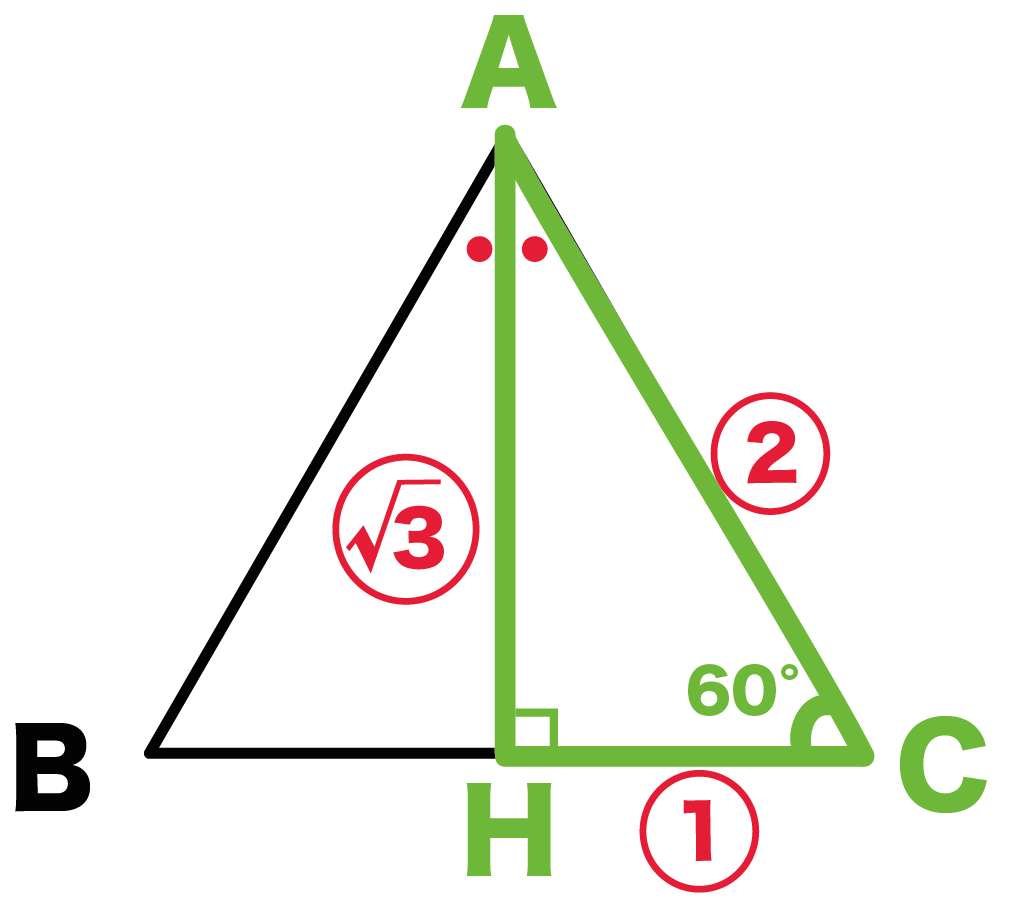
三角形の面積の公式は、「底辺×高さ÷2」です。 「なんで2で割るの?」と聞かれたら、答えは簡単。 「この三角形と同じ三角形を上下ひっくり返してくっつけてごらん。 平行四辺形になったでしょ。この平行四辺形の面積を2で割ればいいんだよ。 1 2 √3 になっているはず。 よって、 高さAH = AC ×√3/2 = 6× √3/2 = 3√3 になるんだ。 メンドイときは正三角形の高さの公式をつかってもいいよ^^ Step3 三角形の面積の公式をつかう! あとは面積の公式で計算するだけ。 公式って、 底辺×高さ÷2 だったよね?先生「三角形の面積は底辺×高さ÷2で導けます」 人間達「三角形を2つ足したら四角形になるから四角形の面積を出して2つに割るからか!」 先生「では次の問題へ進みます」 人間達「はーい!」 ワイ「なんで2で割るんや」 先生「ぺちゃくちゃ」
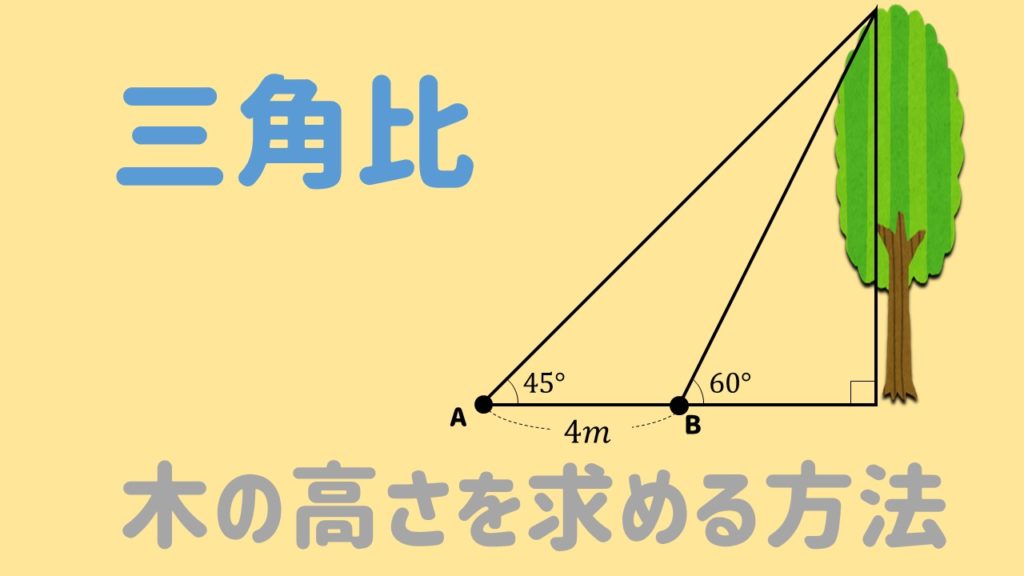



高1数学 木の高さを三角比を用いて求める方法を解説 数スタ
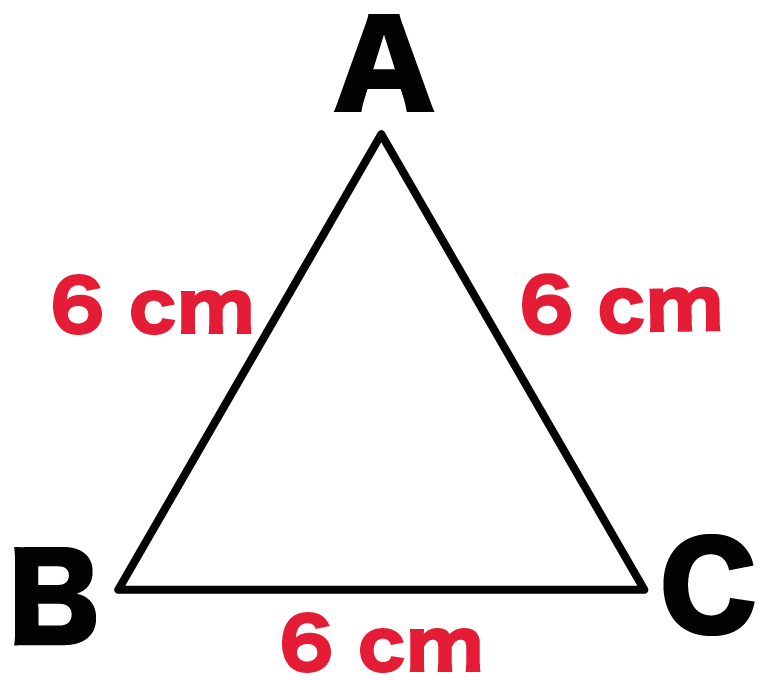



簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
高校2年生の年齢は「16歳~17歳」です。 年度はじめの4月1日は全員16歳で、誕生日を迎えた人から17歳になります。 学年 年齢 高校2年生 16歳 (誕生日がまだの人) 17歳 (誕生日を迎えた人) ※ 現役入学で留年なしの場合。高さ 面積 上底(または下底) が既知のとき計算できます。これは台形の面積を求める式が、 台形の面積=(上底下底)×高さ÷2 のためです。実際に、下図の台形の底辺(下底)を計算します。 面積が30、高さが5、上底が2です。前述した公式に 相似な三角形の面積比 以下の2つの三角形は相似です。 2つの三角形は相似。 相似比は2:3 底辺の比が2:3なら、それぞれの高さの比も2:3です。 ということで 面積比が分かります。 面積の比は2×2:3×3=4:9。 この考え方も「相似比をそれぞれ2回
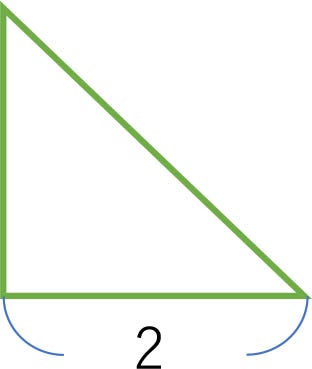



面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱
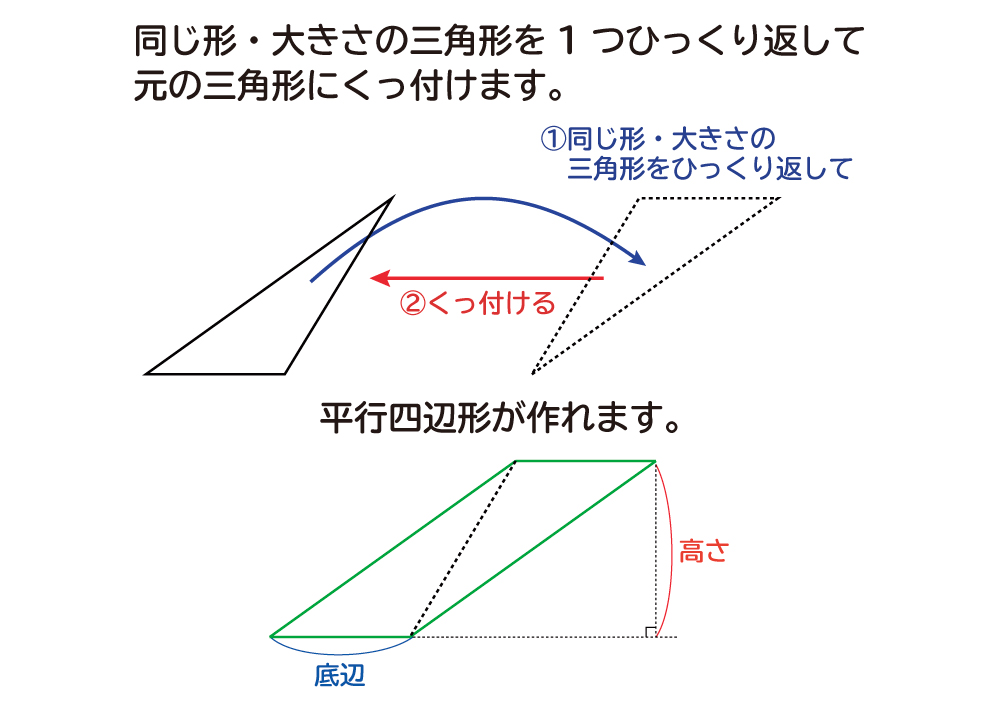



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
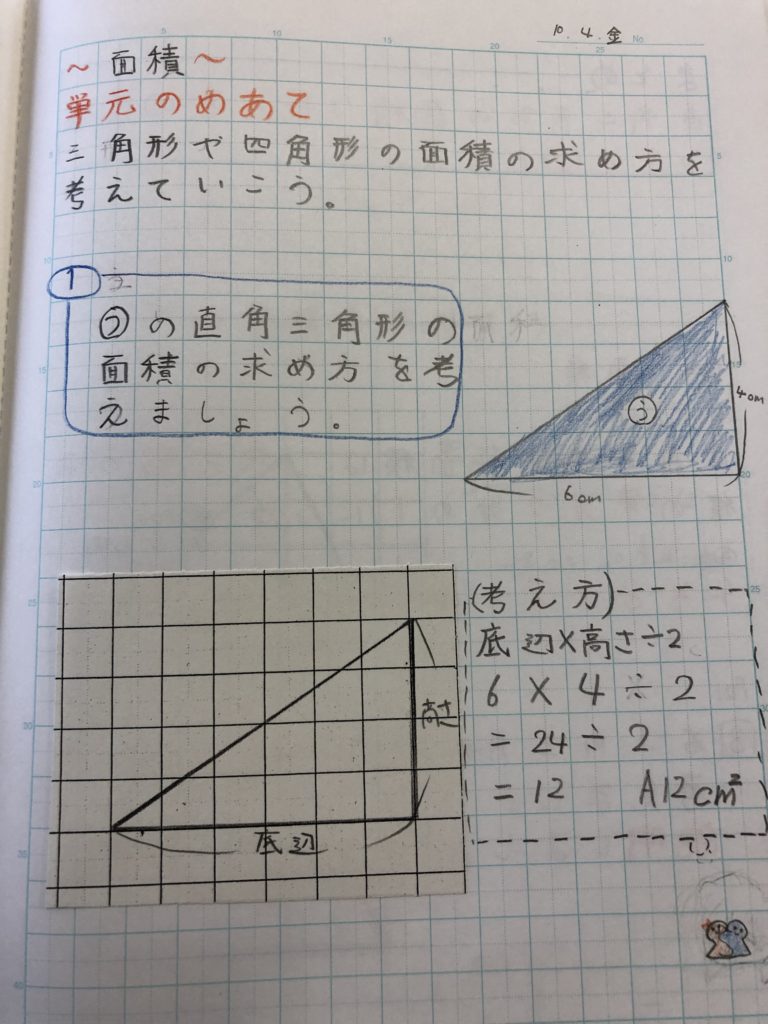
三角形は、高さが同じであれば変形させても面積は変わらないので、②の面積は変わりません。 よって台形の面積の公式「(上底+下底) 高さ÷2」は、三角形の公式「底辺 高さ÷2」と同じになります。 台形の面積 その2 まず台形を用意します。 18年9月26日 / 19年1月3日 三角形の面積は「 底辺 高さ 底 辺 × 高 さ ÷ 2 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていき②高さを cm,面積を ㎠として,底辺が cmの三角形の面積を 求める式を書きましょう。 ( × ÷ 2= ) ③面積が ㎠のとき,高さは何cmですか。 式 × ÷ 2= ( 5 cm ) × = × 2 = ÷ = 12 12 30 12 30 60 5 12 30 12 面積 (㎠) 6 12 18 ものです。次の問題に答えましょう。




三角形の面積の公式の導き方 8種類 算数を究める




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
右と左の2辺と底辺は分かっています。 どうか回答お願いします。 補足 小学6年生の問題です。 三角形の面積を求める公式(底辺 × 高さ ÷ 2 )を 教えなくても解けている。 。 。 基本の次くらいのレベル⁈では パパより、補助線をひいて考えてみてとアドバイス受け 解けて褒められムスメさんドヤ顔 三角形の面積は元になる四角形の面積の半分三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度
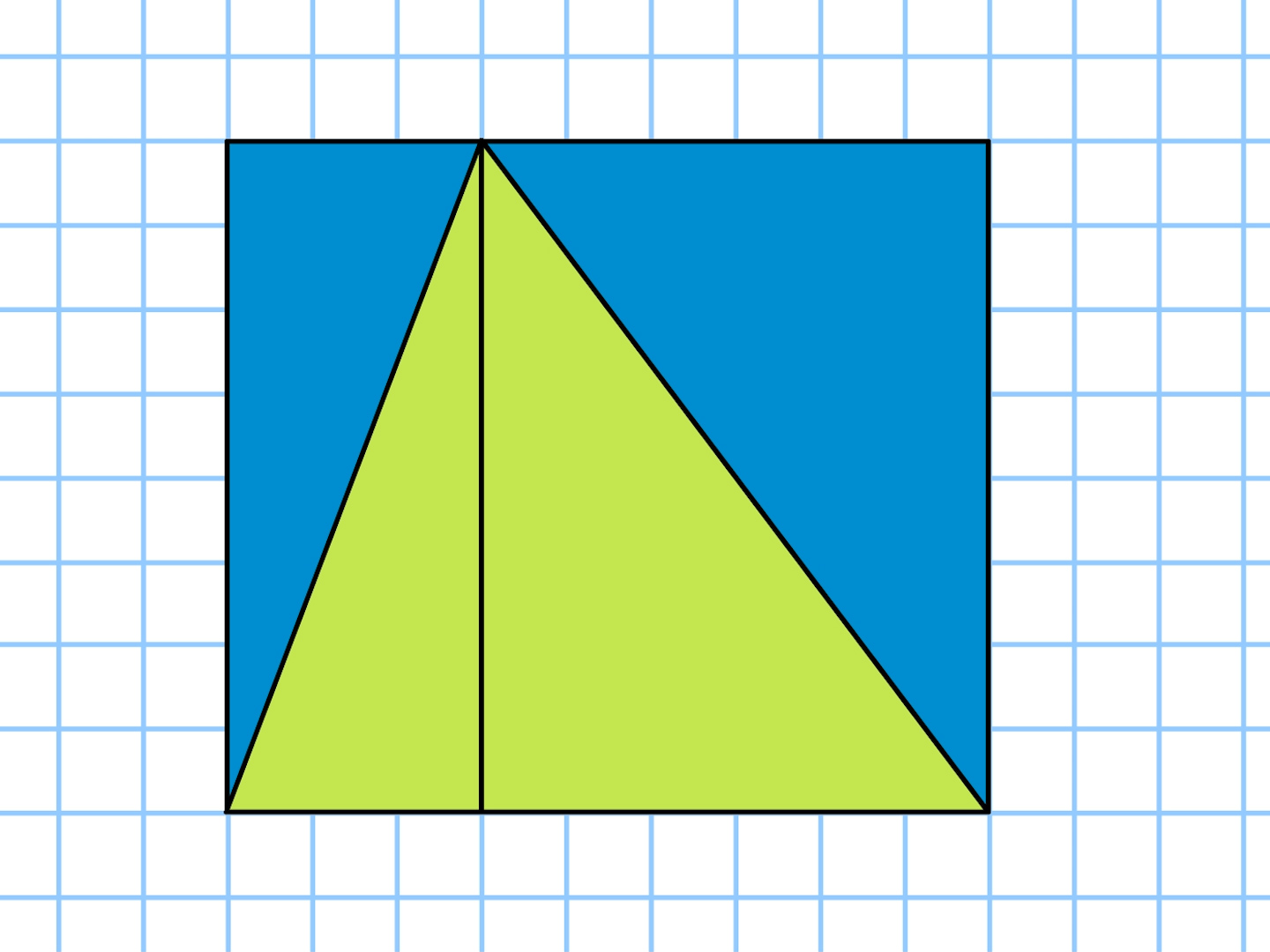



5年 三角形の面積 算数イメージ動画集 大日本図書
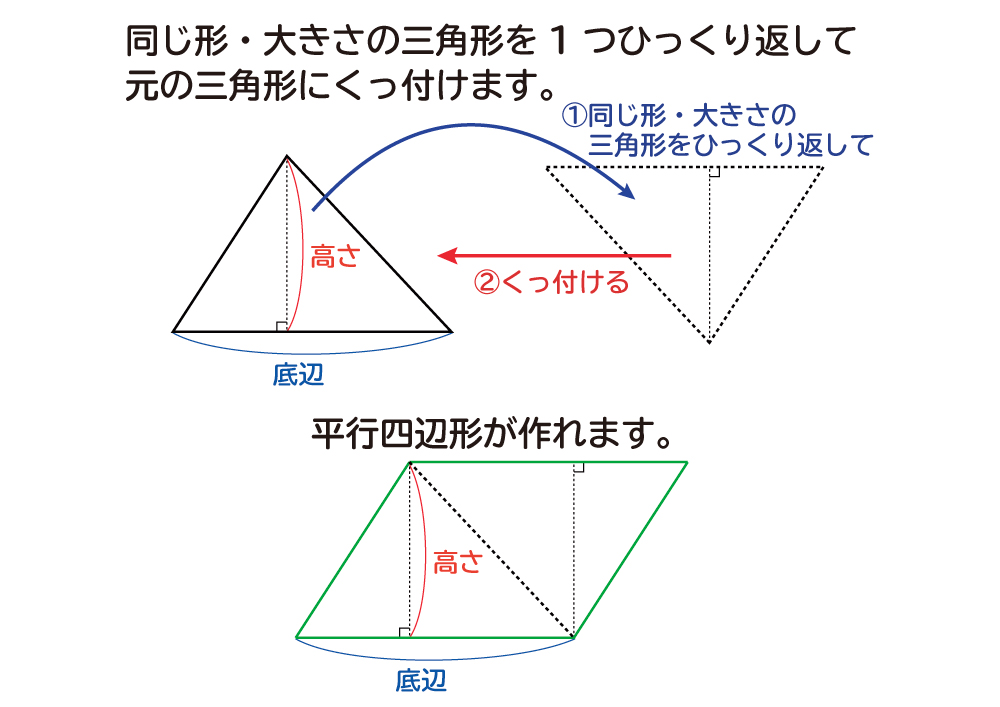



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
tae******** さん 1718 5 回答 三角形について質問です。 三角形の (底辺)x (高さ)÷2はわかるのですが、高さがわからない時はどうやって求めるのですか?底辺×高さ÷2で①の面積を求めることができます。 鋭角三角形 下図の様に補助線を引きます。 鋭角三角形は直角三角形が二つあると考えると分かりやいです。 鈍角三角形 このような鈍角三角形の面積は「底辺×高さ÷2」で説明できるのでしょうか。 もう一つ鈍角三角形の面積が底辺×高さ÷2を導いてみたいと思います。 先程と同じ下の図を使います。 この鈍角三角形の面積は、大きな直角三角形から小さな直角三角形を引いて求めることができます。 青い三角形=(底辺横)×高さ÷2 ピンクの三角形=横×高



簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



5年算数 四角形と三角形の面積 教え方
年2月21日 0803 初めに「底辺」ありきで、それにより「高さ」が存在します。 だから「底辺×高さ」です。 かけ算は、かける数とかけられるさて、今回は私が高校生のとき、先生から聞いた話を紹介したいと思います。 高校3年生、理科(地学)の最後の授業で、先生は私たちに 「理科が嫌いな子どもたちを育てないでくれ。」 と言いました。 「子どもには絶対、『なんで?』を連発する時期がある。 先生「三角形の面積は底辺×高さ÷2で導けます」人間達「はーい! 同じ三角形をもう一つ用意して切り貼りしていけば、三角形の底辺と高さを2辺とする長方形になるじゃん 高専卒業して2年目だけど同い年が就職で喘いでるの見ると高専ってイージー




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




体積について 小学校算数 中学校数学から 身勝手な主張
対角線A×対角線B÷2 どちらも意味は同じです。 正方形は長方形でありひし形なので両方の面積の公式が使えるわけです。 これはよくポイントになります。 また上の2つ以外にも対角線が垂直に交わる通称「たこ形」という図形も同じ公式が使えます




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays




三角形の面積の公式の導き方 8種類 算数を究める
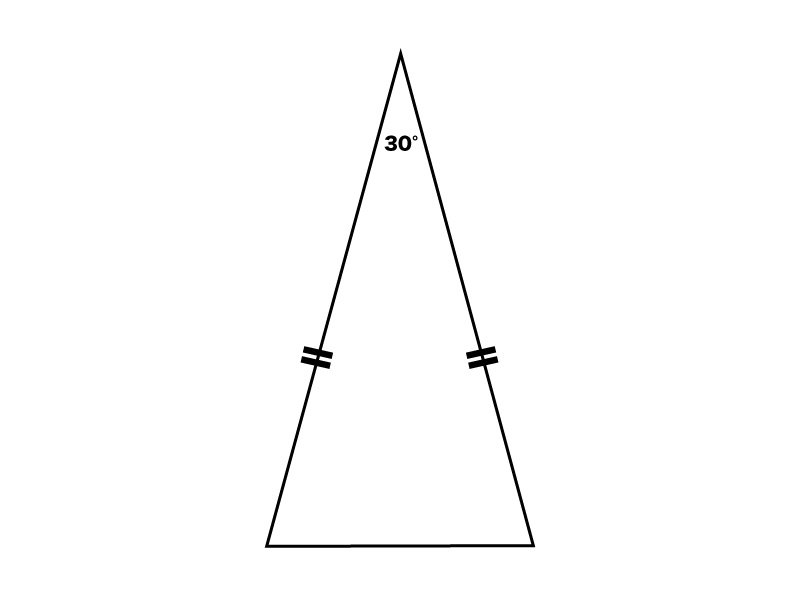



30 二等辺三角形の謎公式 斜辺 斜辺 4 って何 受験算数入門




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
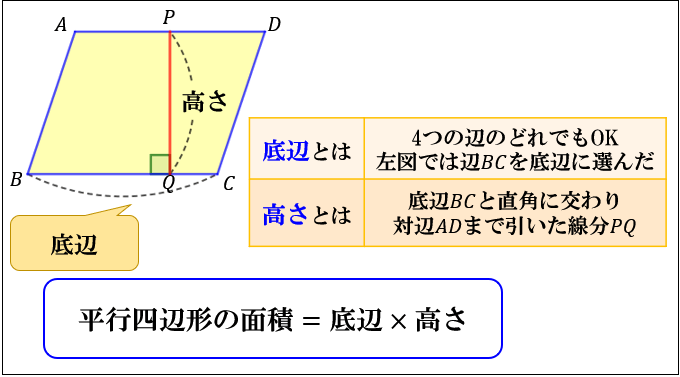



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




三角形の面積の公式の導き方 8種類 算数を究める




世界一分かりやすい算数 小5 面積



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
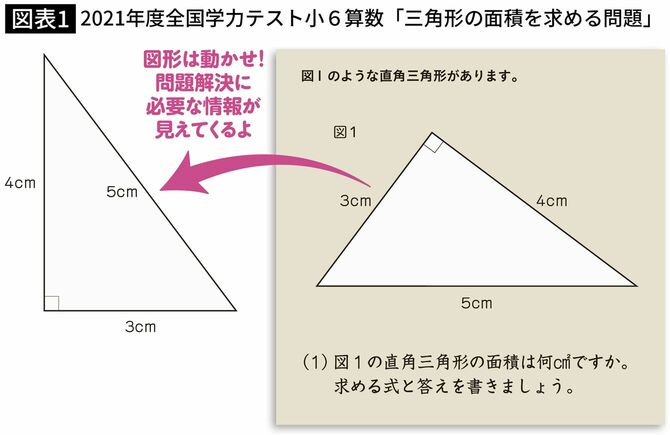



正解率は55 教育界に激震 小6が直角三角形の面積を求める問題に大苦戦する理由 図形オンチが1日で解消するドリル President Online プレジデントオンライン



三角形の底辺の長さを求めましょう 高さ4 面積8 です 小学5年生に Yahoo 知恵袋




小学5年生 三角形の面積 算数 Active Learning 学院




面積の公式は1つでいい 万能な公式を紹介します 算数を究める




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



小学5年生の娘の問題です 下記の問題の 底辺の長さが分かりません 5年 Yahoo 知恵袋
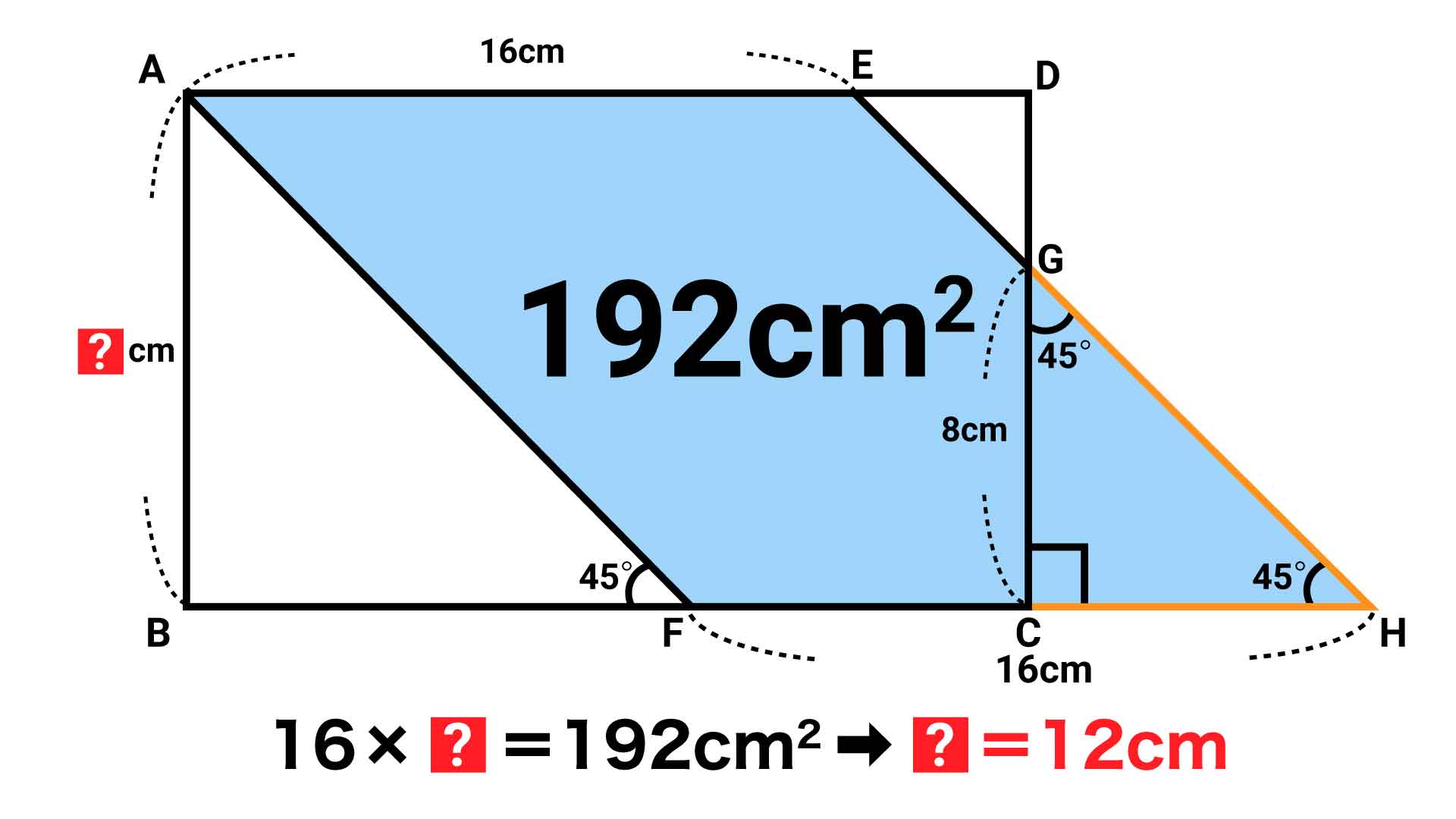



小学5年生レベルの 長さを求める問題 あなたは解けますか
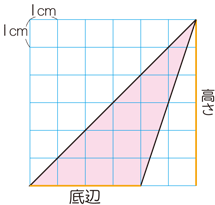



底辺と高さ 算数用語集
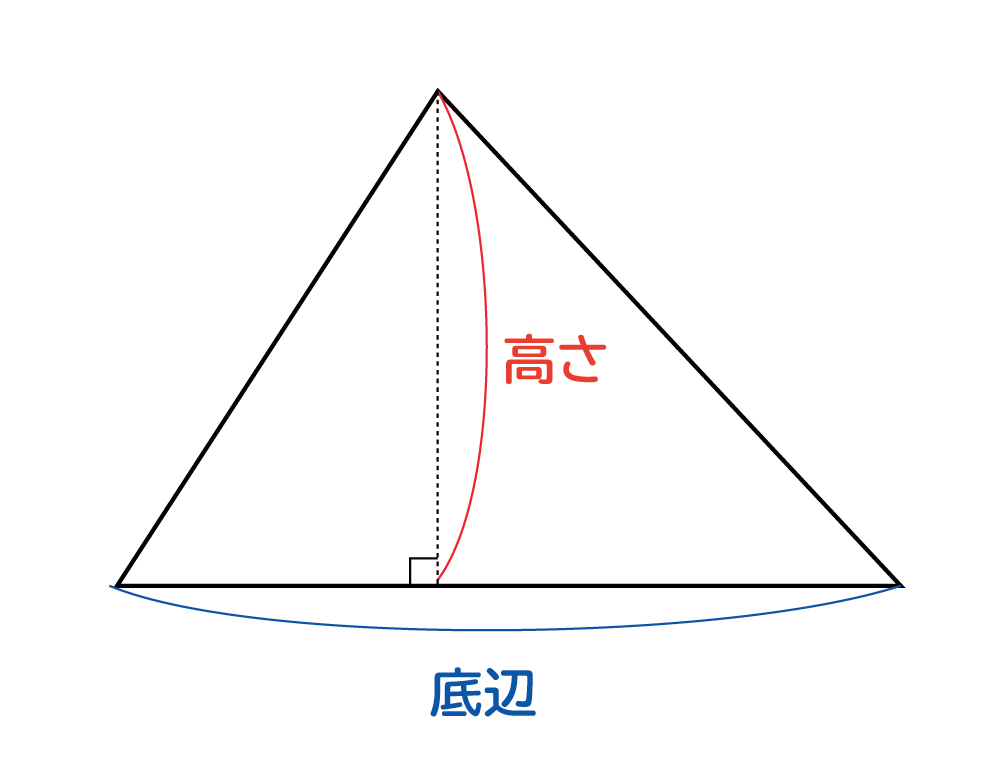



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




小5 算数 小5 45 高さと面積の関係 Youtube
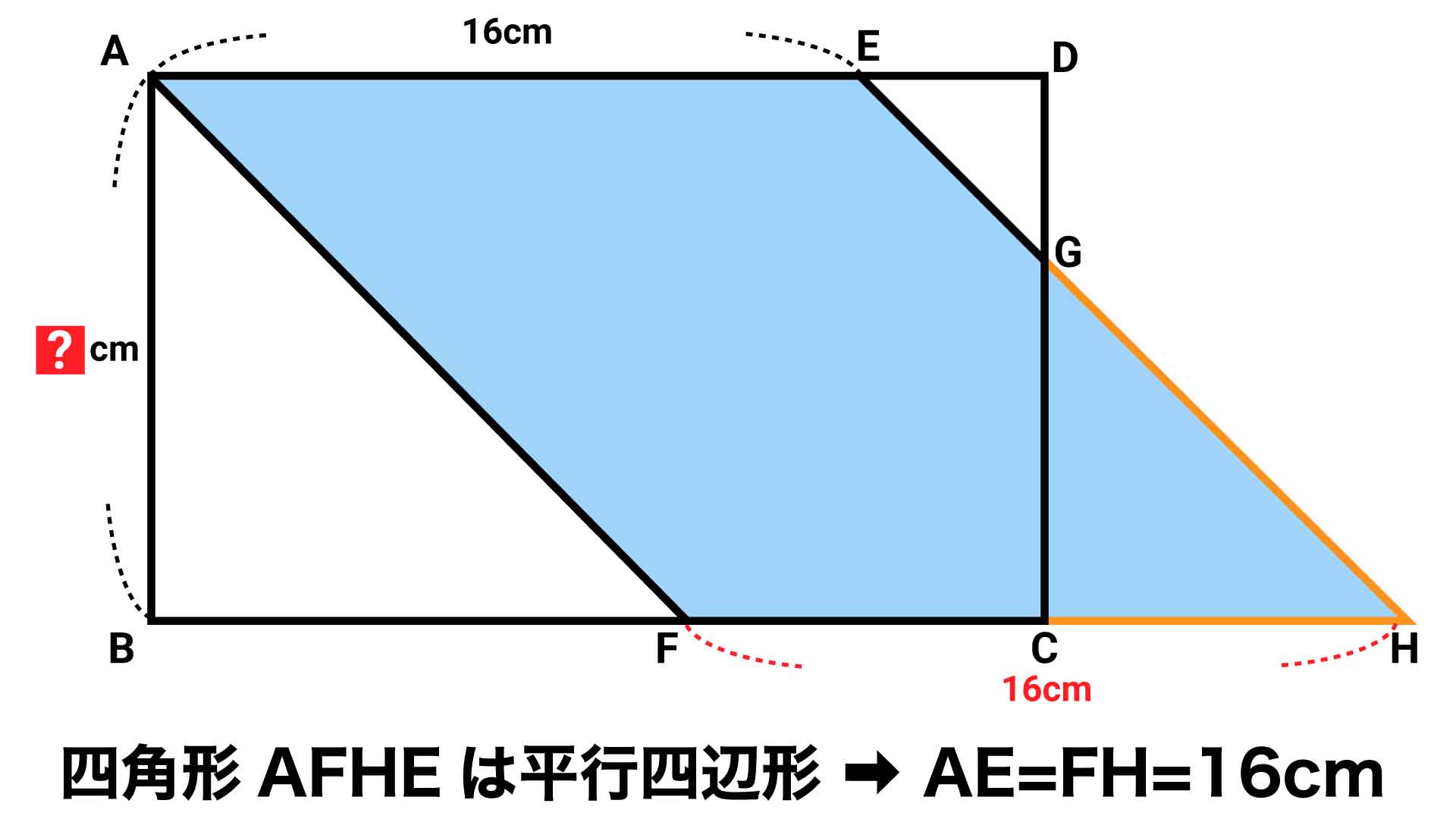



小学5年生レベルの 長さを求める問題 あなたは解けますか



小学5年生の算数の問題です どうしても子供の宿題が解けず こちらに Yahoo 知恵袋
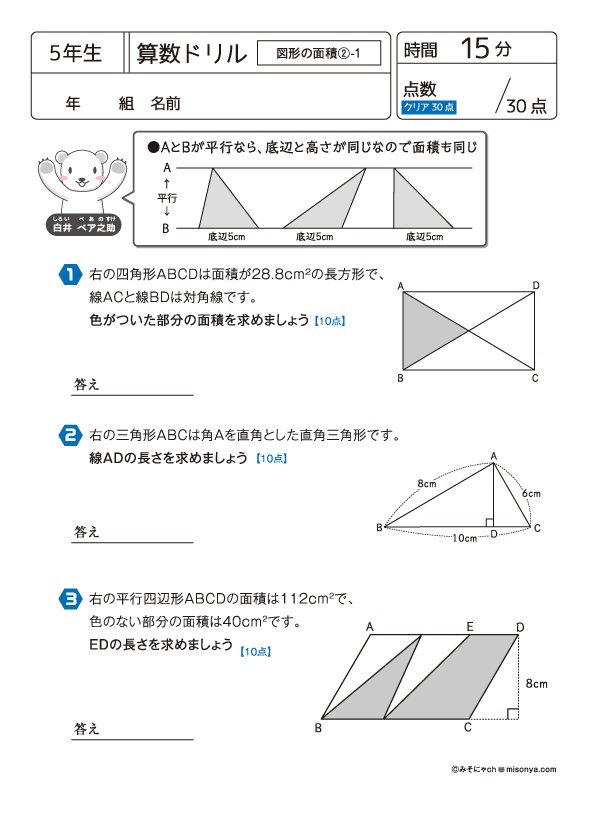



無料の学習プリント 小学5年生の算数ドリル 図形の面積2 みそにゃch




マスラボ 小学5年生 三角形の面積 高さや底辺を求める Youtube
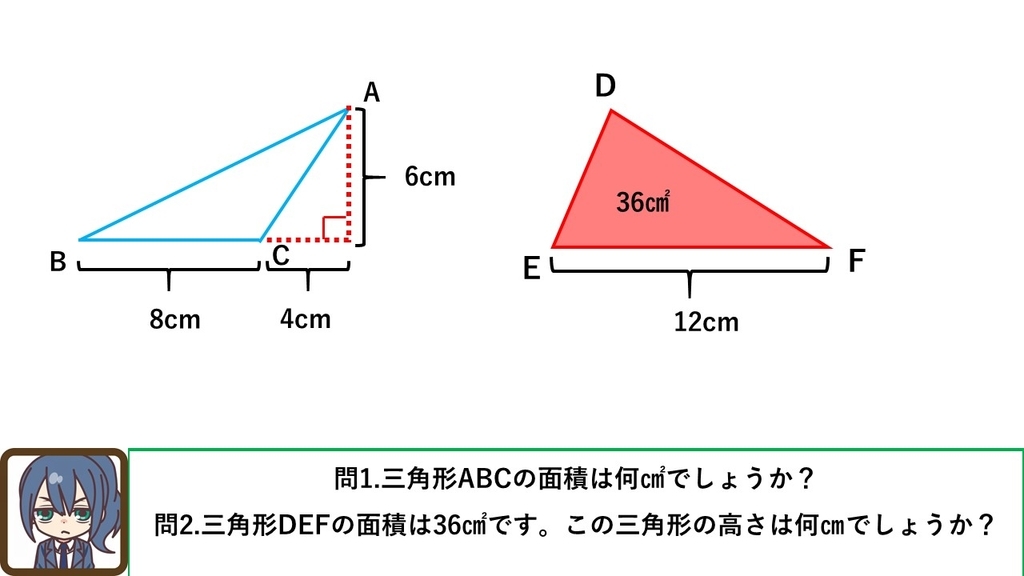



小学5年生 三角形の面積 算数 Active Learning 学院




六角形に接した三角形の面積は 小学6年生レベル ひらめけば瞬殺



小学5年生です この直角三角形の面積を出したいのですが 底 Yahoo 知恵袋




数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
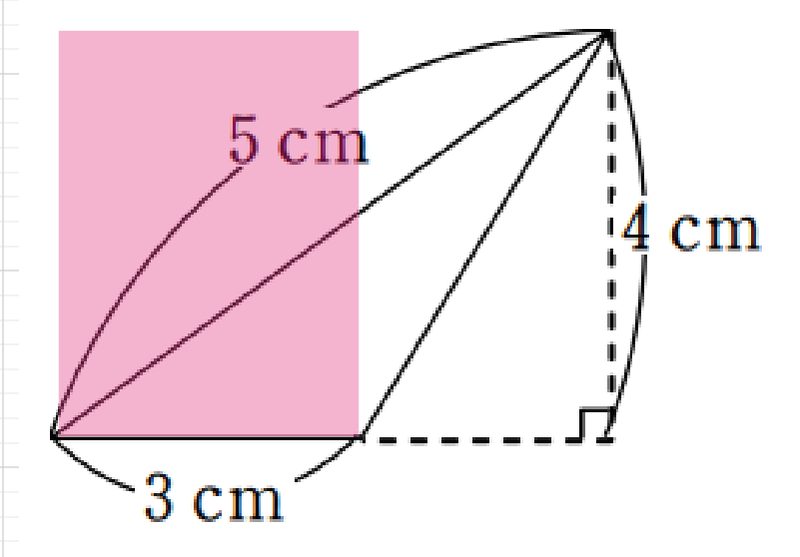



小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays




世界一分かりやすい算数 小5 面積




第13回 平面図形 平行四辺形 三角形 4年生 中学受験walker




底辺6cmの直角三角形があります その三角形の高さを 小学生の知識 数学 教えて Goo
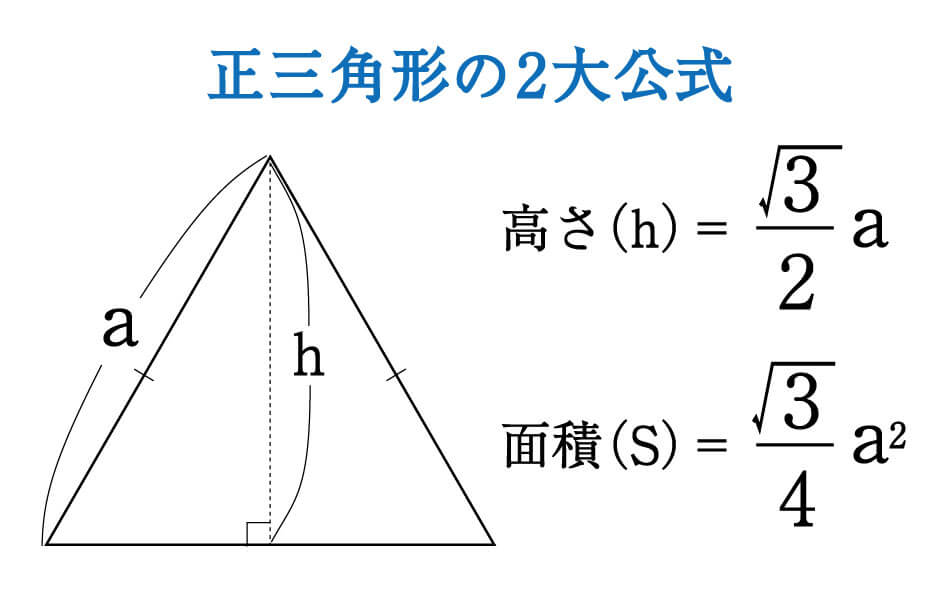



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角形の面積の公式の導き方 8種類 算数を究める
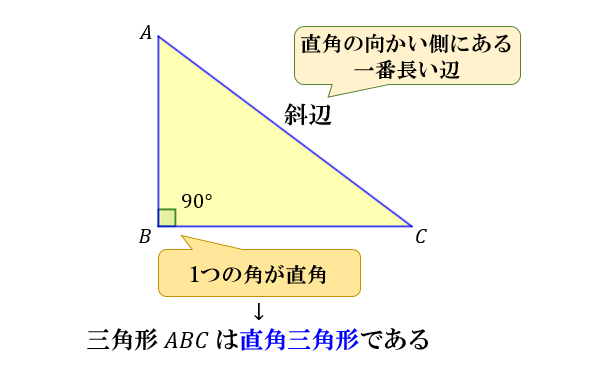



直角三角形の辺の長さ 合同条件 面積について アタリマエ
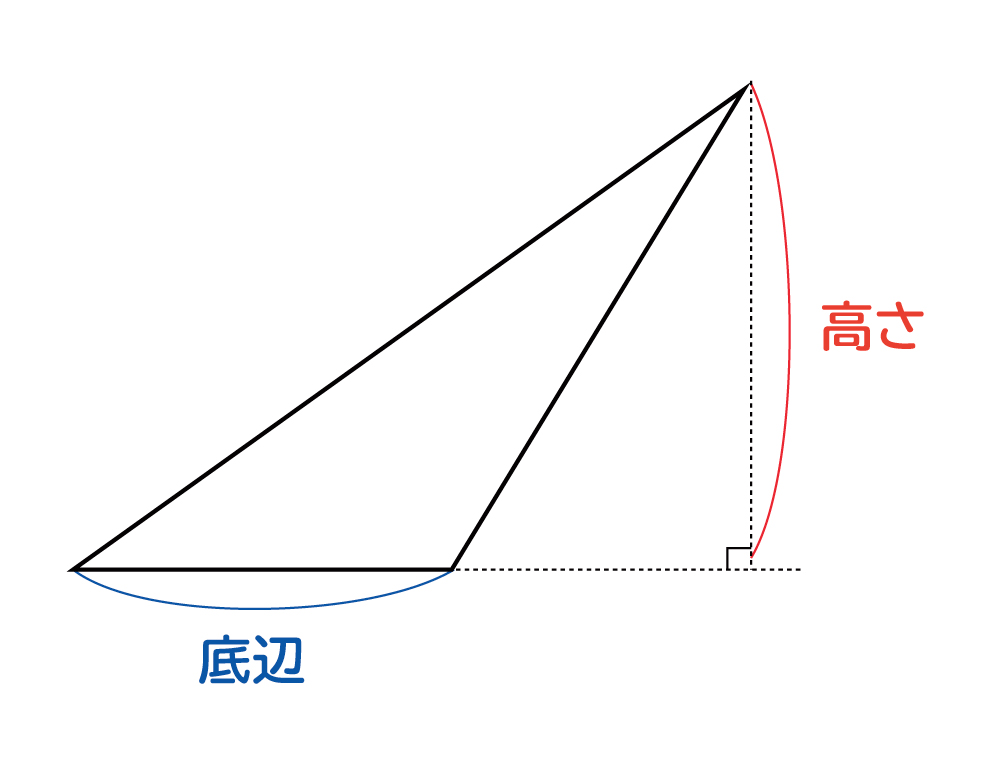



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




三角形の面積の公式 2 って どうして2で割るの




小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays
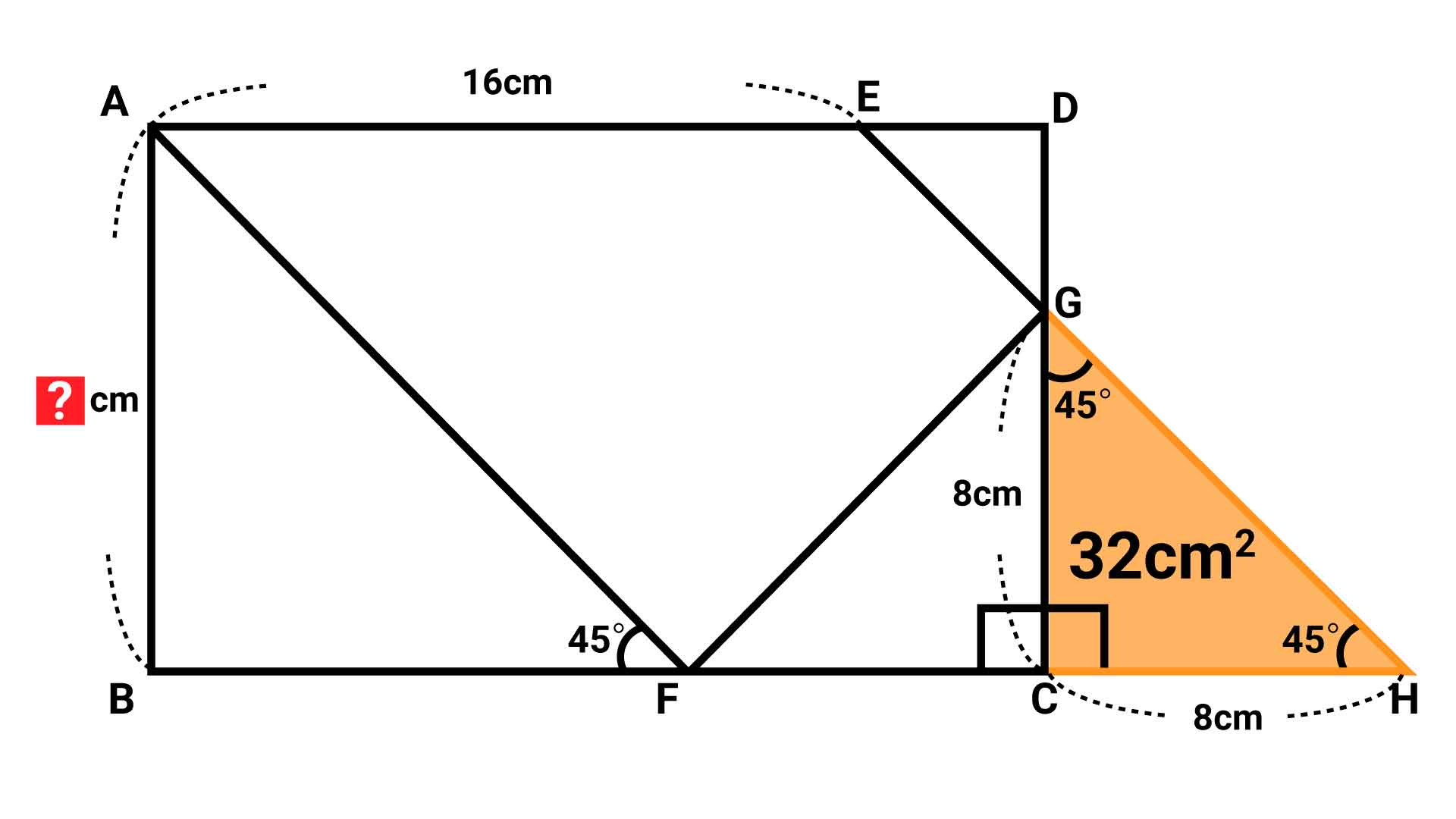



小学5年生レベルの 長さを求める問題 あなたは解けますか
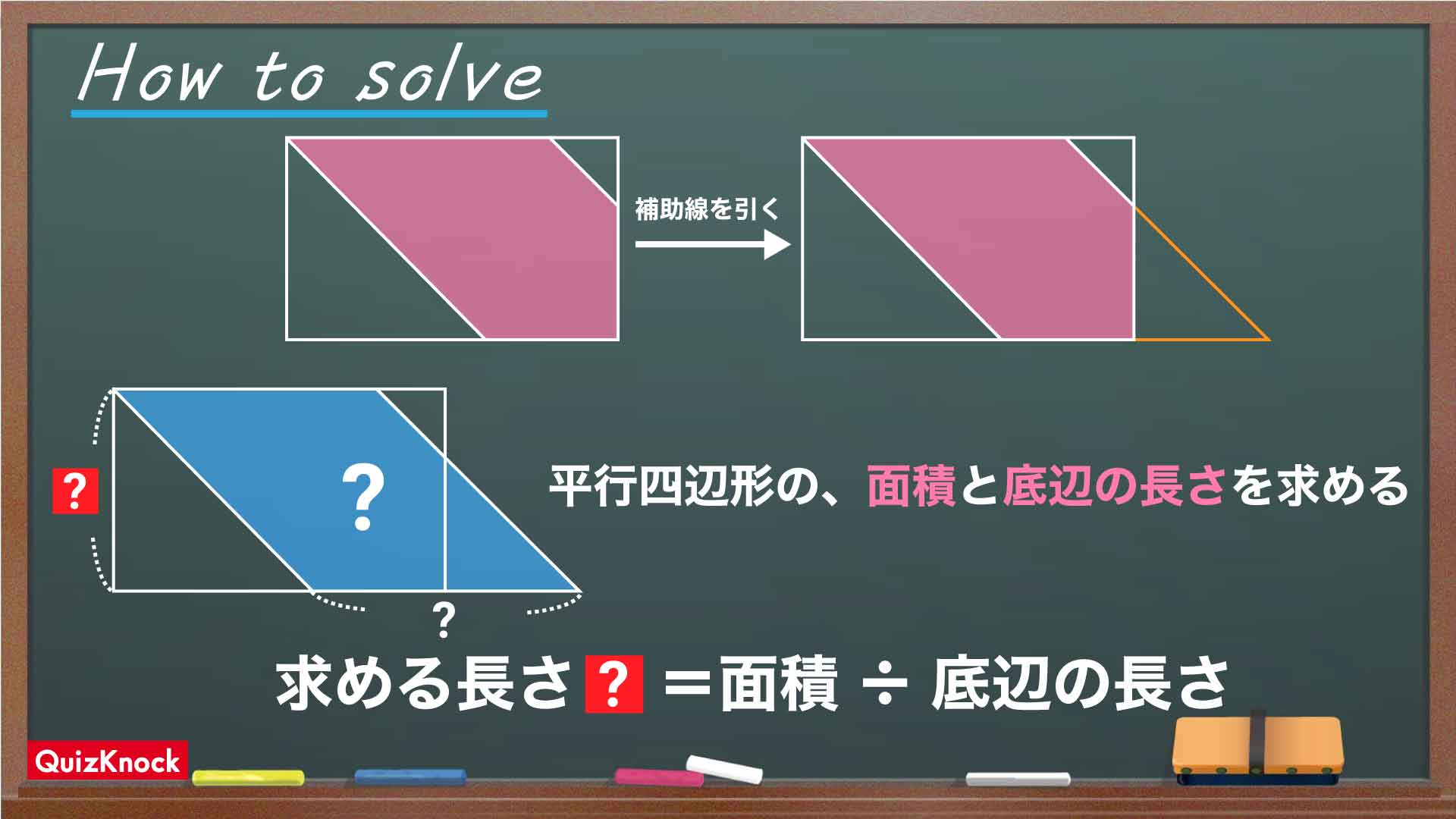



小学5年生レベルの 長さを求める問題 あなたは解けますか




平行四辺形の面積の求め方 公式と計算例
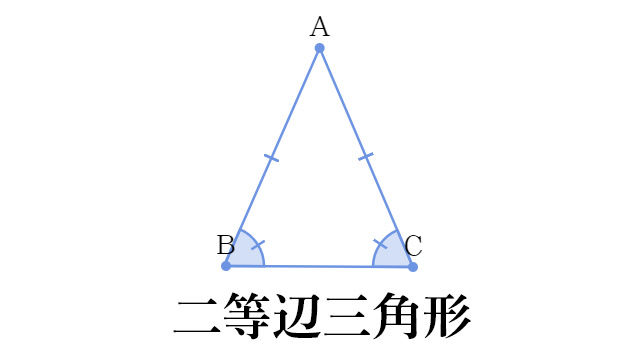



今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
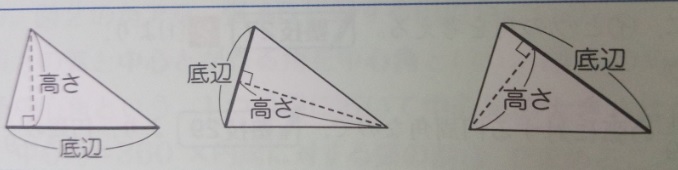



三角形の面積 中学受験 塾なし の勉強法
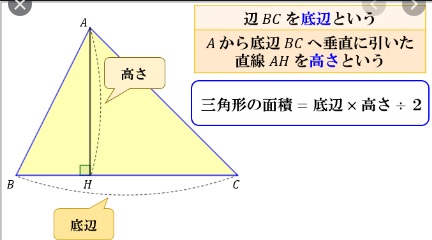



三角形の面積 中学受験 塾なし の勉強法
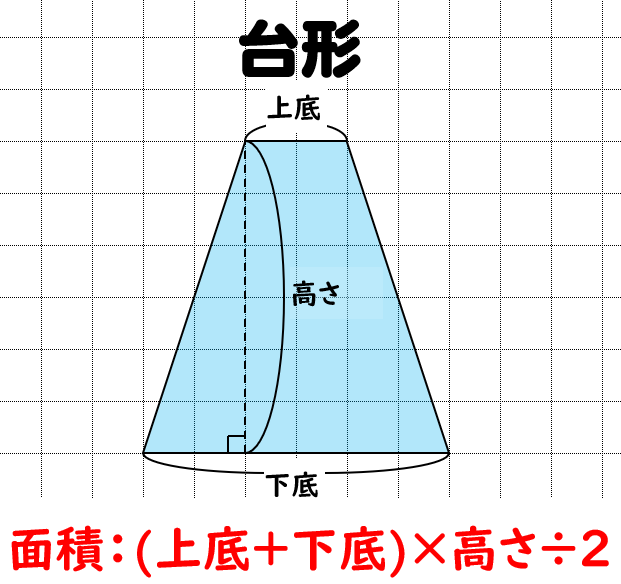



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




名門国立小のカリスマ先生に聞く なんでこれがわからないの でイラっときた時の教え方 Forbes Japan フォーブス ジャパン




面積 平行四辺形の面積 01 高さが外にあるときの面積の求め方 Youtube
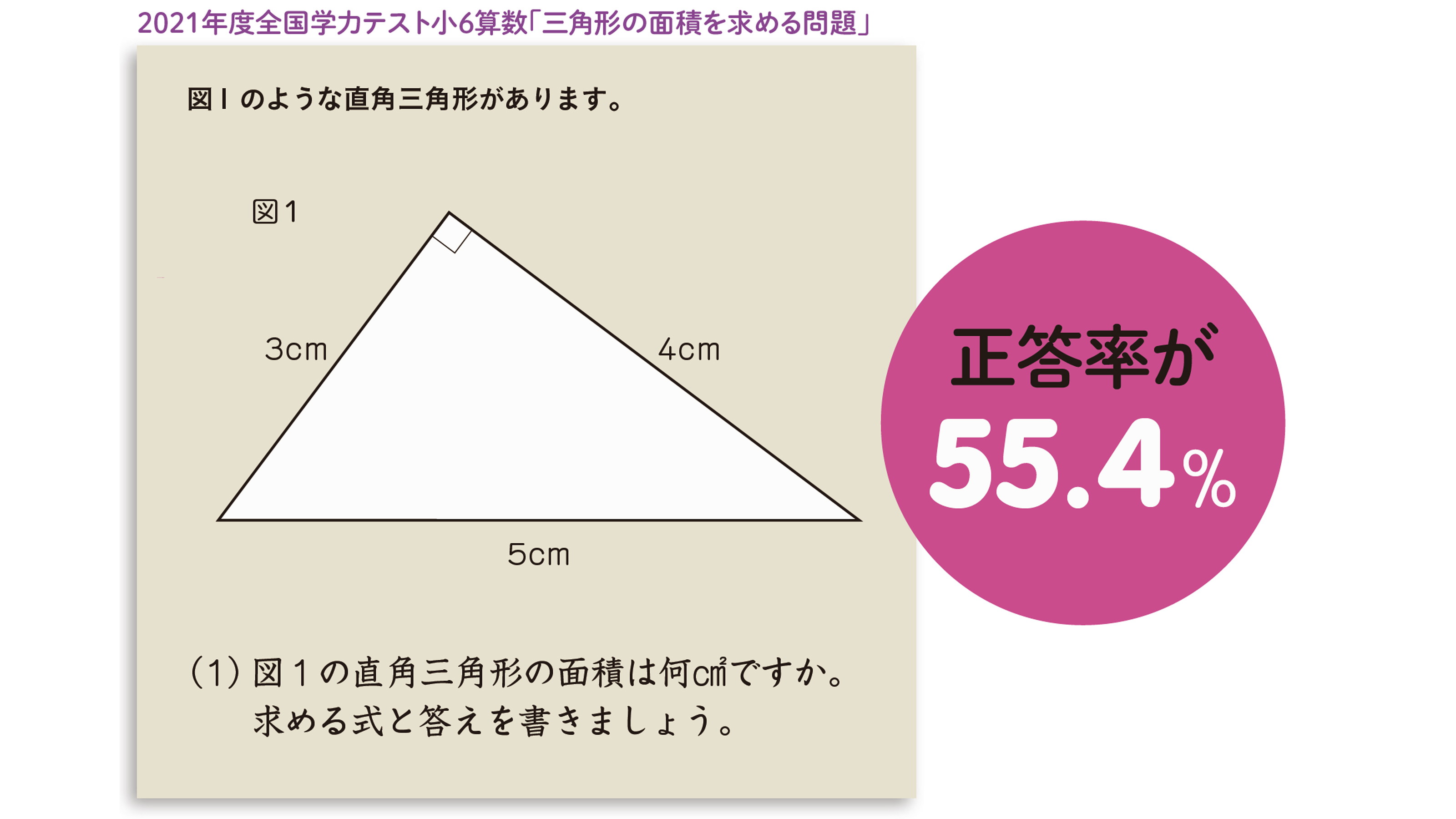



正解率は55 教育界に激震 小6が直角三角形の面積を求める問題に大苦戦する理由 図形オンチが1日で解消するドリル President Online プレジデントオンライン



三角形の高さを求めましょう底辺3 5 面積7 小学5年生にわかるようにお願いし Yahoo 知恵袋



再投稿 台形の高さの求め方小5の算数です底辺の長さが24cm 高さが Yahoo 知恵袋




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
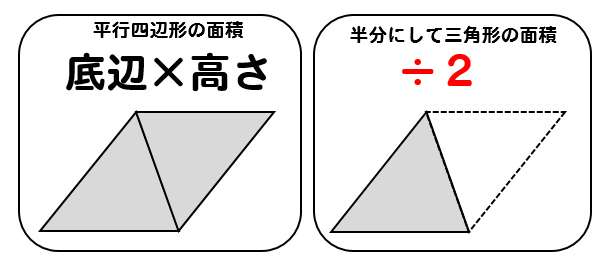



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
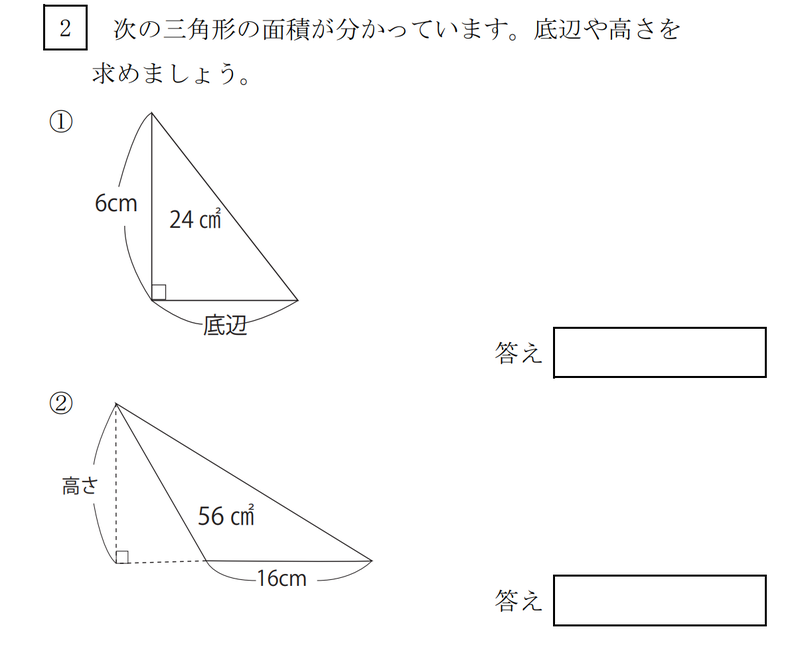



小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays



3




Page 2 2 円の面積はなぜ 半径 半径 3 14 仕組み がわかれば算数は面白い ダ ヴィンチweb



余弦定理



1




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
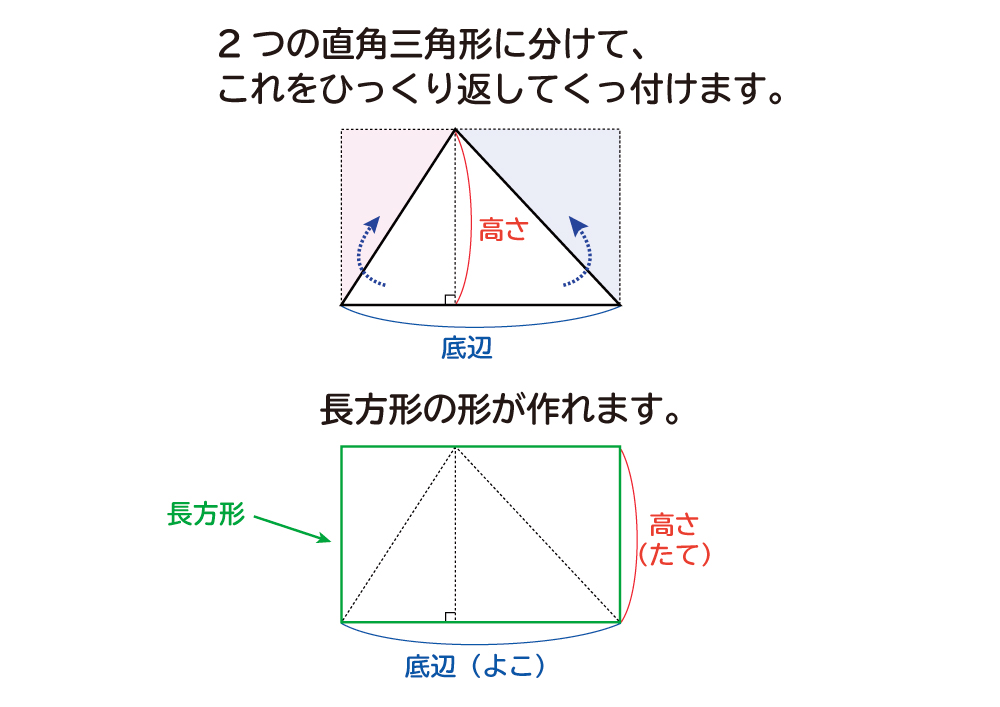



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
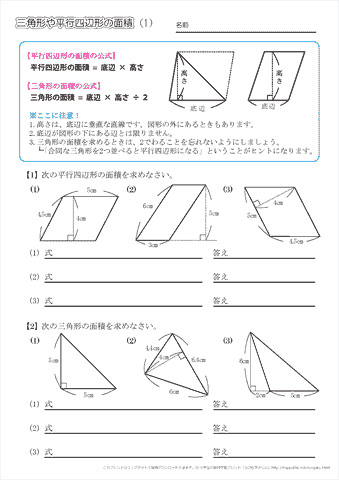



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



三角形と台形の面積




小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays




台形の中の三角形の面積は台形の何倍か 台形の中にある三角形が台形の何倍 Okwave
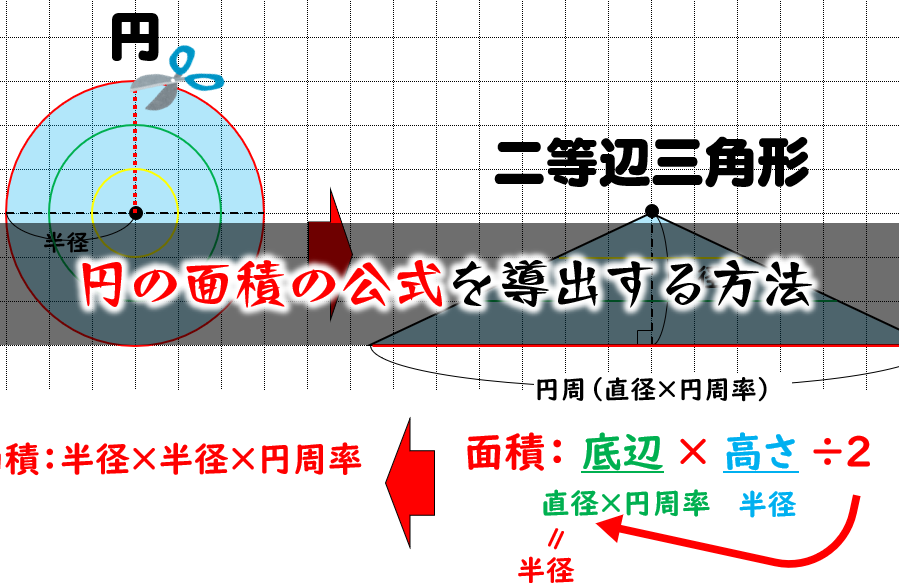



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun
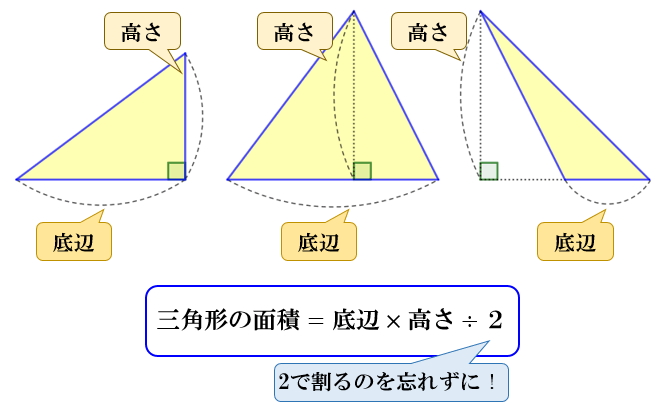



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
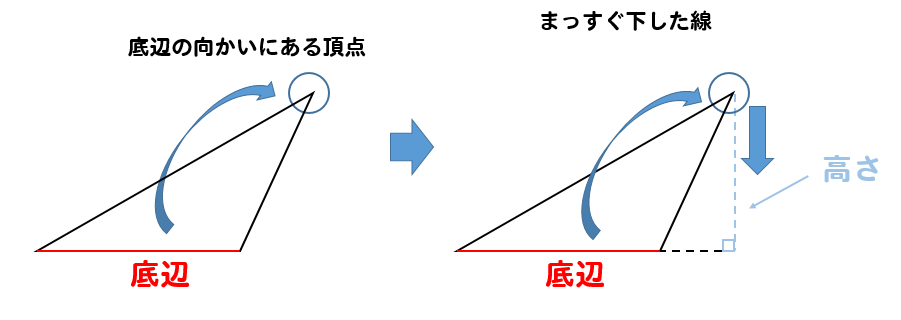



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ
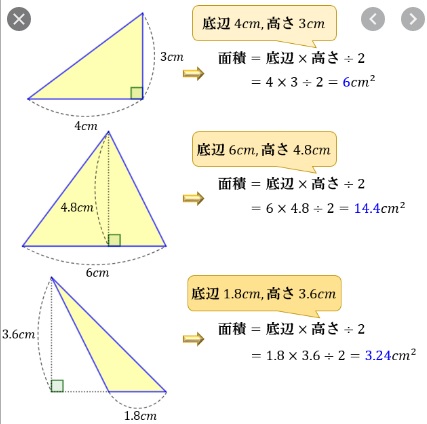



三角形の面積 中学受験 塾なし の勉強法
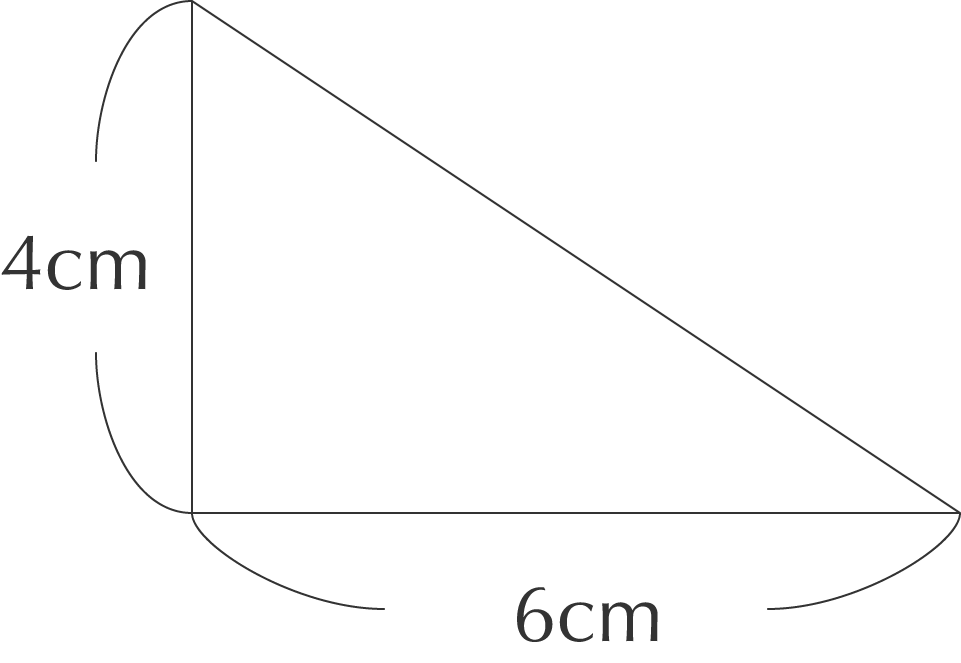



三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook
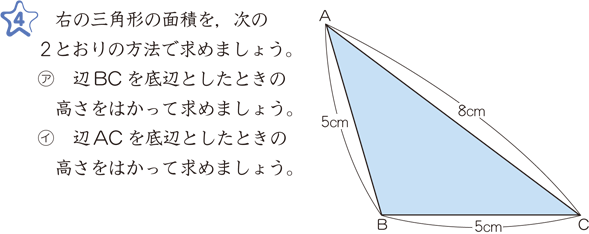



底辺と高さ 算数用語集




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
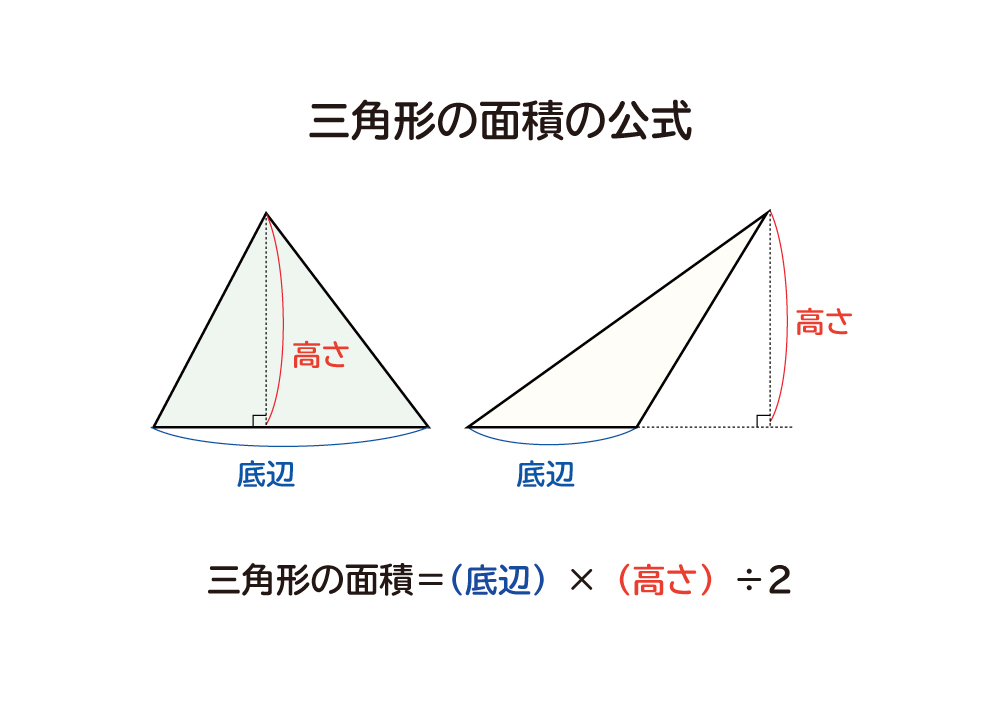



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三角形の面積の公式の導き方 8種類 算数を究める
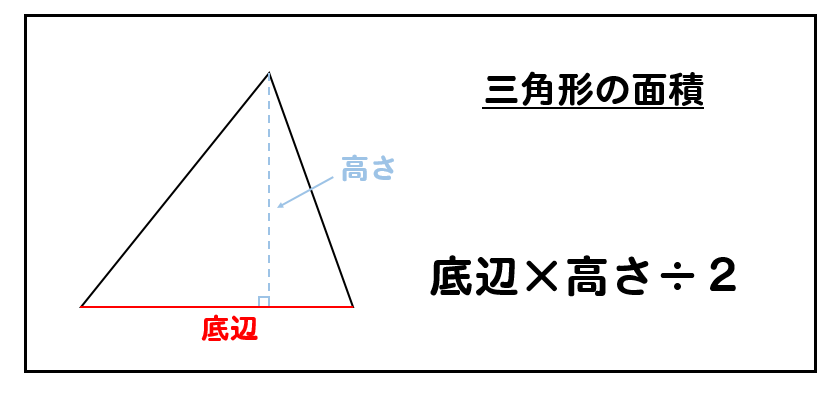



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




平行四辺形の面積の求め方 公式と計算例



小学6年生 算数の問題です 台形abcdの面積の求めかたを詳しく教えて下さい Yahoo 知恵袋
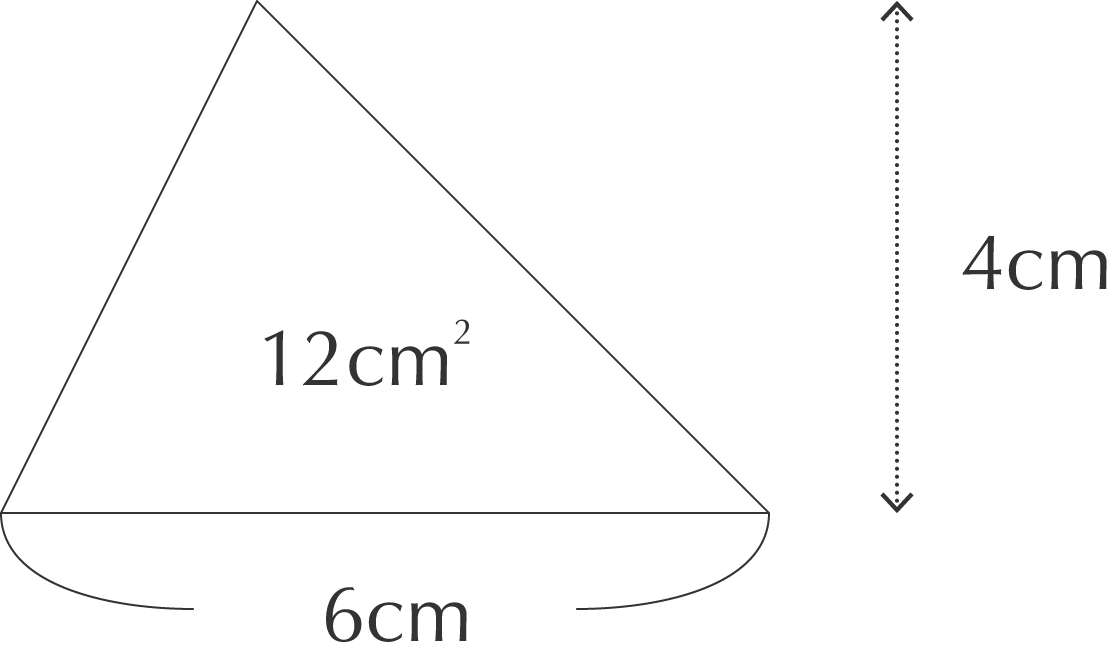



三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook
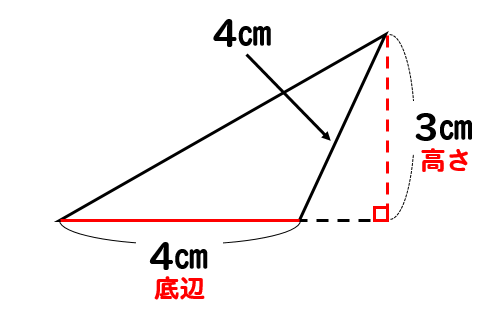



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ
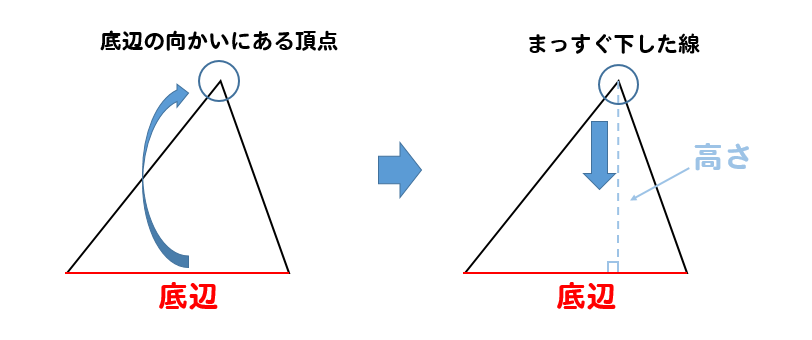



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



0 件のコメント:
コメントを投稿